Construindo uma rede neural

Estou planejando alguns artigos com aplicação de redes neurais, antes melhor explicar os conceitos básicos e suas aplicações, para isso, vamos criar nossa rede neural

Conceitos

Primeiro os conceito do modelo de neurônio que vamos utilizar, e como ele se organiza em estrutura para formar uma rede

Modelo Perceptron

Modelo matemático que recebe valores, multiplicados pelos pesos correspondentes, com os resultados somados e ajustados na saída para 1 ou 0, representado na imagem a seguir:

A estrutura de um neurônio artificial do tipo Perceptron (ou neurônio McCulloch-Pitts)

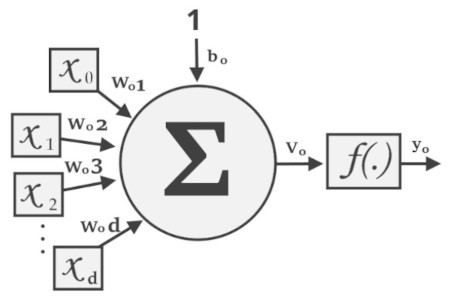
Fonte: adaptado de Silva et al. (2016)

A figura ilustra uma simulação de funcionamento de um neurônio no modelo Perceptron com valores de entrada {x₀, x₁, x₂ ... x_d} sendo multiplicados por pesos sinápticos {w₀₁, w₀₂, w₀₃ ... w_0d}, respectivamente

Esses valores são somados e acrescidos por um valor externo b₀, também um peso, gerando o somatório v₀, aplicado na função f(.) para gerar o valor de saída y₀

Sendo x₀, x₁, x₂ ... x_d, w₀₁, w₀₂, w₀₃ ... w_0d, b₀ e v₀ valores entre 0 e 1, e y₀ com valor de 0 ou 1

A função f(.) é determinada por um valor limiar, dependendo da aplicação, retornando 0 ou 1

Multicamadas

Com aplicação do modelo de neurônio em sequência, com os valores v₀ (somatória) sendo usando para a valor de entrada para outros neurônios

Rede neural com multicamadas de neurônios

Fonte: adaptado de Wikipédia

Cada camada tem uma identificação:

• camada de entrada (input layer): Valores iniciais, vindo pela entrada de dados, pode ser coordenadas, estrutura de uma imagem entre outros;
• camada oculta (hidden layer): As camadas com os neurônios que não são os de entrada e saída;
• camada de saída (output layer): Saída de valores, que podem ter um ou mais saídas todas sendo 0 ou 1.

Implementação

Agora com os conceitos em mão vamos para aplicação, com somente uma camada oculta

Matemática

No exemplo vamos usar uma rede com três (3) neurônios na camada de entrada, cinco (5) na camada oculta e somente dois (2) na camada de saída

Na camada de entrada (layer_input) como parâmetro criamos uma matriz com a quantidade de entradas (3) contendo os valores desejados, exemplo:

A = [0.1, 0.2, 0.3]

Como pesos da camada de entrada (weight_input) devemos ter uma matriz com a quantidade de entradas (3) e quantidade de ocultas (5), exemplo:

B = [
        [0.11, 0.12, 0.13, 0.14, 0.15],
        [0.21, 0.22, 0.23, 0.24, 0.25],
        [0.31, 0.32, 0.33, 0.34, 0.35]
]

Para calcular a saída pesos da camada oculta (weight_hidden) precisamos de uma matriz com dimensões de com quantidade de ocultas (5) e quantidade de saída (2), exemplo:

C = [
        [0.11, 0.12],
        [0.21, 0.22],
        [0.31, 0.32],
        [0.41, 0.42],
        [0.51, 0.52]
]

Para calcular a primeira passagem, da camada de entrada para camada oculta, podemos calcular com multiplicação de matrizes dos valores e pesos de entrada

Lembrando do índice na maioria das linguagens de programação começa com 0, ou seja A[0][1] é igual a a_{1, 2}

Aplicando a multiplicação entre A e B temos:

X = [
    A[0] * B[0][0]  +  A[1] * B[1][0]  +  A[2] * B[2][0],
    A[0] * B[0][1]  +  A[1] * B[1][1]  +  A[2] * B[2][1],
    A[0] * B[0][2]  +  A[1] * B[1][2]  +  A[2] * B[2][2],
    A[0] * B[0][3]  +  A[1] * B[1][3]  +  A[2] * B[2][3],
    A[0] * B[0][4]  +  A[1] * B[1][4]  +  A[2] * B[2][4]
]

Para aplicar essa fórmula, vamos usar o pacote do Python chamada NumPy, temos um artigo para explicar a instalação de pacotes no Python

A função dot realiza um produto de duas matrizes, fazendo uso dela temos

import numpy as np

X = np.dot(A, B)

Assim temos o resultado [0.146, 0.152, 0.158, 0.164, 0.17] na variável X com os valores para camada oculta

Para apurar os resultados finais temos os valores em X que multiplicamos com os pesos em C, com seguinte código

Y = np.dot(X, C)

Assim temos [0.2509, 0.2588] que dependendo do nosso valor de limiar para cada saída, pode resultar cada um como 0 ou 1

Finalmente

Aplicando a função de classificação com os valores limiares

classifier = lambda idx, item: 0 if item <= thresholds[idx] else 1

Organizando o que temos

import numpy as np

def neural_network(layer_input, weight_input, weight_hidden, thresholds):
    layer_hidden = np.dot(layer_input, weight_input)
    layer_output = np.dot(layer_hidden, weight_hidden)

    enumerated = enumerate(layer_output)
    classifier = lambda idx, item: 0 if item <= thresholds[idx] else 1

    return [classifier(i, e) for i, e in enumerated]

Só isso? É... só isso!

Referências

Tweet from Santiago

Deep Learning Book - O Perceptron

But what is a neural network? | Chapter 1, Deep learning

NumPy - numpy.dot